jeena/en.javascript.info

Ilya Kantor 3548cba527 works

2016-07-13 18:15:29 +03:00

17 KiB

Raw Blame History

Recursion and stack

A function solves a task. In the process it can call many other functions. A partial case of this is when a function calls itself.

That's called a recursion.

Recursion is useful in situations when a task can be naturally split into several tasks of the same kind, but simpler. Or when a task can be simplified into an easy action plus a simpler variant of the same task.

Soon we'll see examples.

Recursion is a common programming topic, not specific to Javascript. If you developed in other languages or studied algorithms, then you probably already know what's this.

The chapter is mostly meant for those who are unfamiliar with the topic and want to study better how functions work.

[cut]

Recursive thinking

For something simple to start with -- let's consider a task of raising x into a natural power of n. In other words, we need x multiplied by itself n times.

There are two ways to solve it.

Iterative thinking -- the for loop:

function pow(x, n) {
  let result = 1;

  // multiply result by x n times in the loop
  for(let i = 0; i < n; i++) {
    result *= x;
  }

  return result;
}

alert( pow(2, 3) ); // 8

Recursive thinking -- simplify the task:

function pow(x, n) {
  if (n == 1) {
    return x;
  } else {
    return x * pow(x, n - 1);
  }
}

alert( pow(2, 3) ); // 8

The recursive variant represents the function as a simple action plus a simplified task:

            if n==1  = x
             /
pow(x, n) = 
             \       = x * pow(x, n - 1)
            else

Here we have two branches.

The n==1 is the trivial variant. It is called the base of recursion, because it immediately produces the obvious result: pow(x, 1) equals x.
Otherwise, we can represent pow(x, n) as x * pow(x, n-1). In maths, one would write xⁿ = x * x^n-1. This is called a recursive step, because we transform the task into a simpler action (multiplication by x) and a simpler call of the same task (pow with lower n). Next steps simplify it further and further untill n reaches 1.

We can also say that pow recursively calls itself till n == 1.

For example, to calculate pow(2, 4) the recursive variant does these steps:

pow(2, 4) = 2 * pow(2, 3)
pow(2, 3) = 2 * pow(2, 2)
pow(2, 2) = 2 * pow(2, 1)
pow(2, 1) = 2

A recursive solution is usually shorter.

Here we can write the same using the ternary `?` operator instead of `if` to make it even more terse and still very readable:

```js run
function pow(x, n) {
  return (n == 1) ? x : (x * pow(x, n-1));
}
```

So, the recursion can be used when a function call can be reduced to a simpler call, and then -- to even more simpler, and so on, until the result becomes obvious.

The maximal number of nested calls (including the first one) is called recursion depth. In our case, it there will be exactly n.

The maximal recursion depth is limited by Javascript engine. We can make sure about 10000, some engines allow more, but 100000 is probably out of limit for the majority of them. There are automatic optimizations that help to alleviate this ("tail calls optimizations"), but they are not yet supported everywhere and work only in simple cases.

That limits the application of recursion, but it still remains very wide. There are many tasks where a recursive way of thinking gives simpler code, easier to maintain.

The execution stack

Now let's examine how recursive calls work. For that we'll look under the hood of functions, how they work. The information about a function run is stored in its execution context.

The execution context is an internal data structure that contains details about where the execution flow is now, current variables, the value of this (we don't use it here) and few other internal details.

pow(2, 3)

For instance, for the beginning of the call pow(2, 3) the execution context will store variables: x = 2, n = 3, the execution flow is at line 1 of the function.

We can sketch it as:

Context: { x: 2, n: 3, at line 1 } pow(2, 3)

That's when the function starts to execute. The condition n == 1 is falsy, so the flow continues into the second branch of if:

function pow(x, n) {
  if (n == 1) { 
    return x;
  } else {
*!*
    return x * pow(x, n - 1);
*/!*
  } 
}

alert( pow(2, 3) );

The line changes, so the context is now:

Context: { x: 2, n: 3, at line 5 } pow(2, 3)

To calculate x * pow(x, n-1), we need to run pow witn new arguments.

pow(2, 2)

To do a nested call, Javascript remembers the current execution context in the execution context stack.

Here we call the same function pow, but it absolutely doesn't matter. The process is the same for all functions:

The current context is "laid away" on top of the stack.
The new context is created for the subcall.
When the subcall is finished -- the previous context is popped from the stack, and its execution continues.

The context stack as a list where the current execution context is always on-top, and previous remembered contexts are below:

Context: { x: 2, n: 2, at line 1 } pow(2, 2)
Context: { x: 2, n: 3, at line 5 } pow(2, 3)

Here, the new current execution context is also made bold for clarity.

Note that the context of the previous call not only includes the variables, but also the place in the code, so when the new call finishes -- it would be easy to resume. We use a word "line" in the illustrations for that, but of course in fact it's more precise.

pow(2, 1)

The process repeats: a new subcall is made at line 5, now with arguments x=2, n=1.

A new execution context is created, the previous one is pushed on top of the stack:

Context: { x: 2, n: 1, at line 1 } pow(2, 1)
Context: { x: 2, n: 2, at line 5 } pow(2, 2)
Context: { x: 2, n: 3, at line 5 } pow(2, 3)

There are 2 old contexts now and 1 currently running for pow(2, 1).

The exit

During the execution of pow(2, 1), unlike before, the condition n == 1 is truthy, so the first branch of if works:

function pow(x, n) {
  if (n == 1) { 
*!*
    return x;
*/!*
  } else {
    return x * pow(x, n - 1);
  } 
}

There are no more nested calls, so the function finishes, returning 2.

As the function finishes, its execution context is not needed any more, so it's removed from the memory. The previous one is restored off-top of the stack:

Context: { x: 2, n: 2, at line 5 } pow(2, 2)
Context: { x: 2, n: 3, at line 5 } pow(2, 3)

The execution of pow(2, 2) is resumed. It has the result of the subcall pow(2, 1), so it also can finish the evaluation of x * pow(x, n-1), returning 4.

Then the previous context is restored:

Context: { x: 2, n: 3, at line 5 } pow(2, 3)

When it finishes, we have a result of pow(2, 3) = 8.

The recursion depth in this case was: 3.

As we can see from the illustrations above, recursion depth equals the maximal number of context in the stack.

Note the memory requirements. Contexts take memory. In our case, raising to the power of n actually requires the memory for n contexts, for all lower values of n.

A loop-based algorithm is more memory-saving:

function pow(x, n) {
  let result = 1;

  for(let i = 0; i < n; i++) {
    result *= x;
  }

  return result;
}

The iterative pow uses a single context changing i and result in the process. Its memory requirements are small, fixed and do not depend on n.

Any recursion can be rewritten as a loop. The loop variant usually can be made more effective.

...But sometimes the rewrite is non-trivial, especially when function uses different recursive subcalls depending on conditions and merges their results or when the branching is more intricate. And the optimization may be unneeded and totally not worth the efforts.

Recursion can give a shorter code, easier to understand and support. Optimizations are not required in every place, mostly we need a good code, that's why it's used.

Recursive traversals

Another great application of the recursion is a recursive traversal.

Imagine, we have an company. The staff structure can be presented as an object:

let company = {
  sales: [{
    name: 'John',
    salary: 1000
  }, {
    name: 'Alice',
    salary: 600
  }],

  development: {
    sites: [{
      name: 'Peter',
      salary: 2000
    }, {
      name: 'Alex',
      salary: 1800
    }],

    internals: [{
      name: 'Jack',
      salary: 1300
    }]
  }
};

In other words, a company has departments.

A department may have an array of staff. For instance, sales department has 2 employees: John and Alice.
Or a department may split into subdepartments, like development has two branches: sites and internals. Each of them has the own staff.
It is also possible that when a subdepartment grows, it divides further. For instance, the sites department in the future may be split into teams for siteA and siteB. And they, potentially, can split even more. That's not on the picture, just something to have in mind.

Now let's say we want to get the sum of all salaries. How can we do that?

An iterative approach is not easy, because the structure is not simple. The first idea may be to make a for..in loop over company with nested subloop over 1st level departments. But then we need more nested subloops to iterate over the staff in 2nd level departments like sites. ...And then another subloop inside those for 3rd level departments that might appear in the future? Should we stop on level 3 or make 4 levels of loops? At this point the code becomes not just nonuniversal, but also rather ugly (sure, every programmer tried it).

Let's try recursion. We need to write a function that gets an arbitrary department and then either returns the result immediately or simplifies the task.

As we can see, when our function gets a department to sum, there are two possible cases:

Either it's a "simple" department with an array of people -- then we can sum the salaries in a simple loop.
Or it's an object with N subdepartments -- then we can make N recursive calls to get the sum for each of the subdeps and combine the results.

The (1) is the base of recursion, the trivial case.

The (2) is a recursive step. A complex task is split into subtasks for smaller departments. They may in turn split again, but sooner or later the split will finish at (1).

The algorithm is probably even easier to read from the code:

let company = { // the same object, compressed for brevity
  sales: [{name: 'John', salary: 1000}, {name: 'Alice', salary: 600 }],
  development: {
    sites: [{name: 'Peter', salary: 2000}, {name: 'Alex', salary: 1800 }],
    internals: [{name: 'Jack', salary: 1300}]
  }
};

// The function to do the job
*!*
function sumSalaries(department) {
  if (Array.isArray(department)) { // case (1)
    return department.reduce((prev, current) => prev + current.salary, 0); // sum the array
  } else { // case (2)
    let sum = 0;
    for(let subdep of Object.values(department)) {
      sum += sumSalaries(subdep); // recursively call for subdeps, sum the results
    }
    return sum;
  }
}
*/!*

alert(sumSalaries(company)); // 6700

The code is short and easy to understand (hopefully?). That's the power of recursion. It also works for any level of subdepartment nesting.

Note that it uses smart features that we've covered before:

Method arr.reduce explained in the chapter info:array-methods to get the sum of the array.
Loop for(val of Object.values(obj)) to iterate over object values: Object.values returns an array of them.

Recursive structures

A recursive (recursively-defined) data structure is a structure that replicates itself in parts.

We've just seen it in the example of a company structure above.

A company department is:

Either an array of people.
Or an object with departments.

A more familiar example for web-developers would be an HTML or XML document.

In the document, an HTML-tag may contain a list of:

Text pieces.
HTML-comments.
Other HTML-tags (that in turn may contain text pieces/comments or other tags etc).

That's once again a recursive definition.

There exist other structures as well, and we can create them by ourselves where convenient.

Linked list

For instance, we want to store an ordered list of objects.

The natural choice would be an array:

let arr = [obj1, obj2, obj3];

...But there's a problem with arrays. The "delete element" and "insert element" operations are expensive. For instance, arr.unshift(obj) operation has to renumber all elements to make room for a new obj, and if the array is big, it takes time.

Actually, the only structural modifications that do not require mass-renumbering are those that operate with the end of array: arr.push/pop.

So, an array has drawbacks.

Alternatively, if we really need fast insertion/deletion, we can choose another data structure called a linked list.

The linked list element is recursively defined as an object with:

value.
next property referencing the next list element if exists or is null otherwise.

For instance:

let list = {
  value: 1,
  next: {
    value: 2,
    next: {
      value: 3,
      next: {
        value: 4,
        next: null
      }
    }
  }
};

Graphical representation of the list:

An alternative code for creation:

let list = { value: 1 };
list.next = { value: 2 };
list.next.next = { value: 3 };
list.next.next.next = { value: 4 };

Here we have multiple objects, each one has the value and next pointing to the neighbour. The list variable is the first object in the chain.

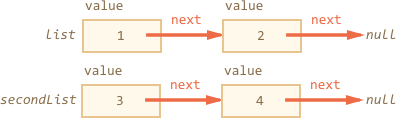
The data structure is interesting, because it can be easily split into multiple parts. For instance:

let secondList = list.next.next;
list.next.next = null;

Later lists can be easily joined by changing next back:

list.next.next = secondList;

And surely we can insert or remove items in any place.

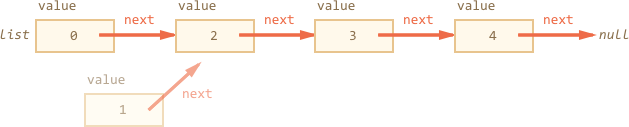
For instance, to prepend a new value to the list:

let list = { value: 1 };
list.next = { value: 2 };
list.next.next = { value: 3 };
list.next.next.next = { value: 4 };

// now list starts with value:0
list = { value: 0, next: list };

To remove a value from the middle, change next of the previous one:

list.next = list.next.next;

Now list.next jumps over to value 2. The value 1 is excluded from the chain. If it's not stored anywhere else, it will be automatically removed from the memory.

We now don't have mass-renumbering and can easily rearrange elements.

But it's a trade-off, because:

We can't easily access an element by a number. We need to start from the first one list and go next N times to get the Nth element.
To insert or remove an element from the structure, we must first get the reference to its previous neighbour, and then alter its next.

...But sometimes these drawbacks do not matter. For instance, when we need a deque: the ordered structure that must allow very fast adding/removing elements from both ends. For that we can add another variable named tail to track the last element of the list (and update it when adding/removing elements from the end).

Summary

[todo better summary]

Recursion -- is when a function calls itself, usually with other arguments.

There are many applications of recursive calls:

Solving complex tasks by splitting into one or several simpler tasks.
Dealing with recursively-defined data structures, like HTML documents or trees.
For "deep" cloning or inspection of complex objects.
...etc

17 KiB Raw Blame History